我院苑光辉教授课题组提出计算平面超构器件矢量衍射场的普适模型 [2025-09-25]

 近期，我院苑光辉教授课题组在国际光学期刊《Journal of Physics: Photonics》上发表题为 “Generic full-vector angular spectrum method for calculating diffraction of arbitrary electromagnetic fields” 的理论研究论文。该研究提出了一种基于快速傅里叶变换的矢量角谱模型，填补了平面超构器件在高数值孔径条件下矢量衍射建模的空白，为复杂光场调控提供了新的理论工具和计算途径。

 对任意矢量光场进行准确的衍射建模，是设计平面超构透镜与实现光波前调控的基础问题。近年来，衍射神经网络、伴随优化等优化算法的出现，进一步推动了厘米尺度多功能超构透镜的实现与设计。然而，大尺寸超构器件通常仍需借助时域有限差分法（FDTD）或近似衍射方法进行模拟与验证。尤其是在高数值孔径平面超构透镜中，其聚焦性能与现有衍射模型的预测结果之间存在显著偏差：传统角谱衍射模型无法解释焦点的不对称性并且无法可靠地预测电场纵向场分布；而经典的理查德—沃尔夫矢量衍射积分（Richard-Wolf diffraction integral）公式仅使用于无球差物镜聚焦系统。因此，开发一种既能保证计算效率又具备高精度的矢量衍射模型，已成为一项迫切需求。

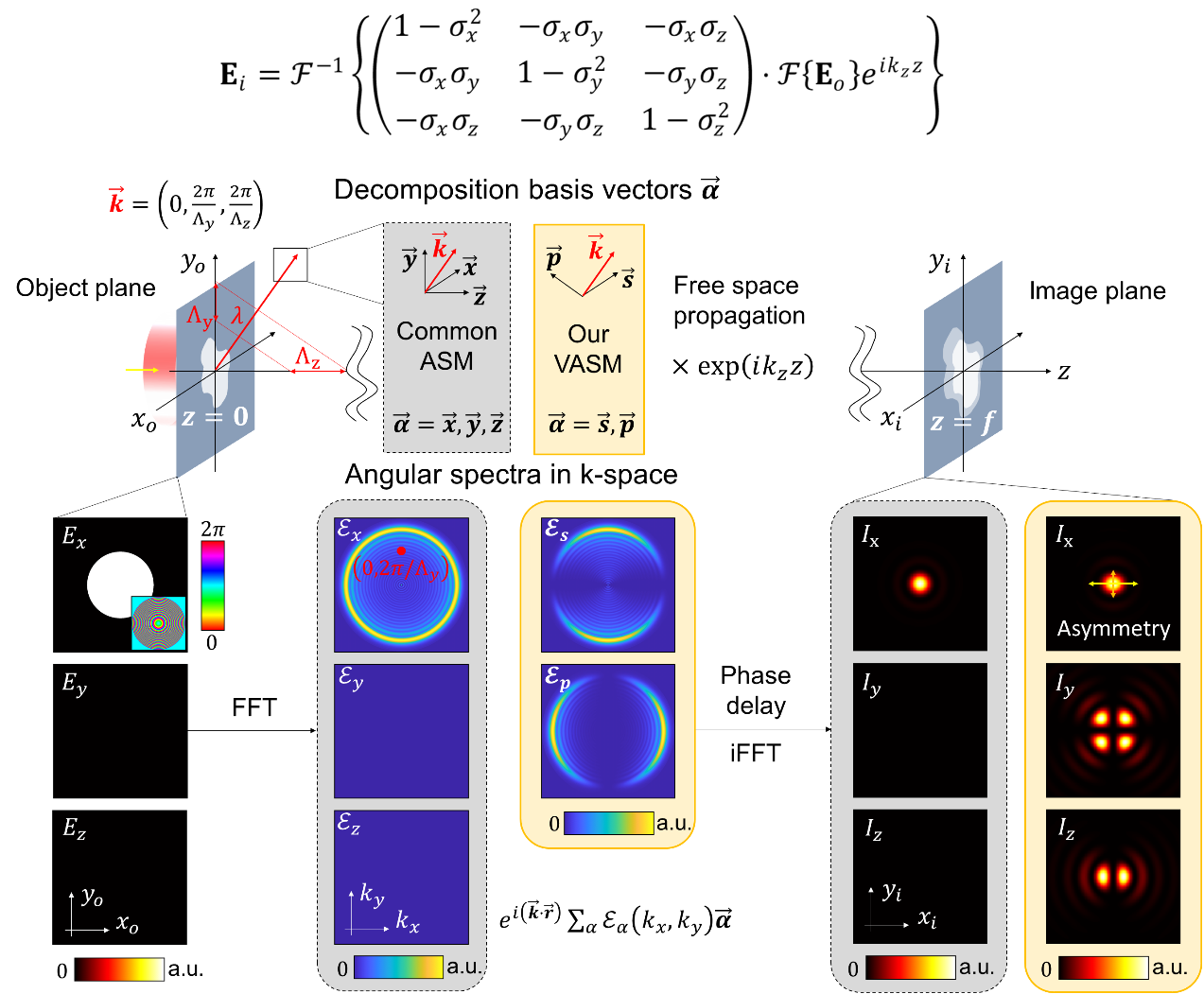
 图一：矢量角谱衍射模型

 针对传统角谱模型中的零散度约束，研究团队受理查德—沃尔夫积分公式中坐标投影思想的启发，构建了适用于任意入射场的矢量角谱模型（图一）。该模型在动量空间中将入射场分解至两个本征横向偏振方向，天然满足了零散度物理约束。数学形式上，该模型将零散度约束包含在3×3偏振投影矩阵中，从而清晰地描述了笛卡尔坐标下各偏振分量之间的耦合与转化行为，可以视为标量角谱方法的一种非退化形式。理论上，该模型仅需输入一个电场分量，即可计算出自洽的全部六个电磁分量的衍射场分布。

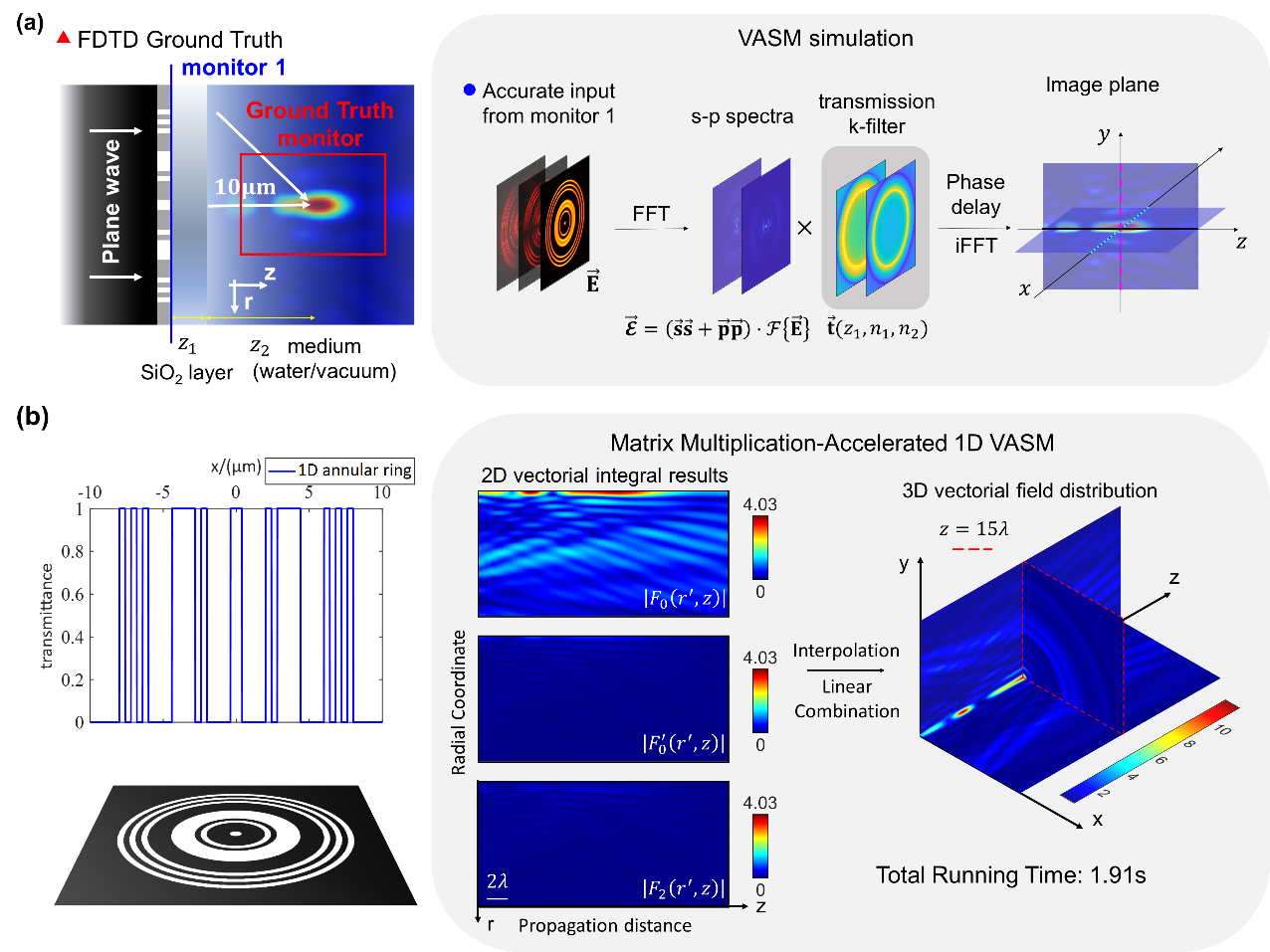
图二：时域有限差分——矢量角谱混合方案与基于矩阵乘法的加速积分策略

 在计算效率与鲁棒性方面，研究团队提出了时域有限差分——矢量角谱混合方案（图二a），兼具高精度、快速和可调性。对于一维径向对称平面器件，团队还开发了基于矩阵乘法的加速积分策略，能够在秒量级内完成尺度为200×200×200网格的三维衍射场计算（图二b），在迭代优化算法中极具应用潜力。

该研究成功修正并拓展了传统角谱模型，不仅增强了对矢量波前的调控与设计能力，还深刻揭示了该模型在动量空间中的线性本质。同时，研究中采用的时域有限差分——矢量角谱混合方案具有良好的鲁棒性、抗噪性和收敛性，在大尺寸光学掩模矢量场快速精确模拟（如光刻）、高数值孔径平面透镜设计、界面透反射分析等领域具有广泛的应用前景，并有望为紧聚焦矢量光场调控研究提供关键基础工具。

 中国科学技术大学博士研究生宋承达为论文第一作者，博士研究生贺竞为论文共同作者。中国科大苑光辉教授为该论文通讯作者。该研究获中国科学院稳定支持基础研究领域青年团队项目（No. YSBR-049）和国家创新人才计划青年项目等支持。

 论文链接：https://iopscience.iop.org/article/10.1088/2515-7647/ae0384